Neural Network Initialization Coverage
Initialization Gone Wrong
Adhitya Arif Wibowo
27 April 2025
1 Preamble
The Universal Approximation Theorem state that we can approximate any continuous function using Neural Network as explained beautifully in below video by Luis Serrano:
As powerful as it is, training Neural Network is hard, even before going through the training process, we need to be careful with the initialization of the parameters. One aspect of it is the parameters’ distribution as discussed here by Andrej Karpathy:
But to me, these ideas seem counter intuitive in that if Neural Network is very powerful, why bother with initialization at all?. In this article, I would like to try to give a very simple counter example to my own intuition doubt, that things can go wrong if a neural network is not initialized properly.
2 Data
We are going to approximate a simple quadratic function with some additional noise below:
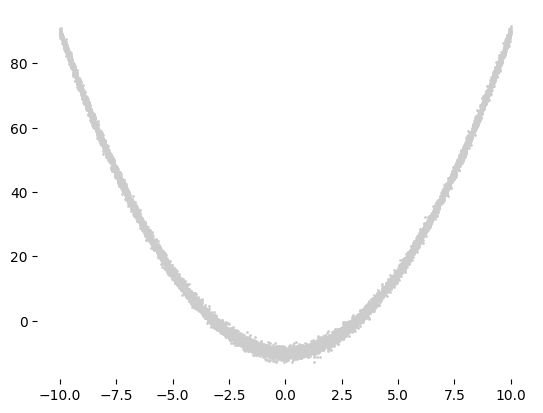
\(f(x)=x^2 - 10 + e\), where \(x\in[-10,10]\) and \(e \sim N( 0, 1 )\) that is \(e\) is normally distributed random number with mean 0 and standard deviation of 1.
3 Setup
We have a 2 layered Neural Network with 2 hidden nodes as follows:
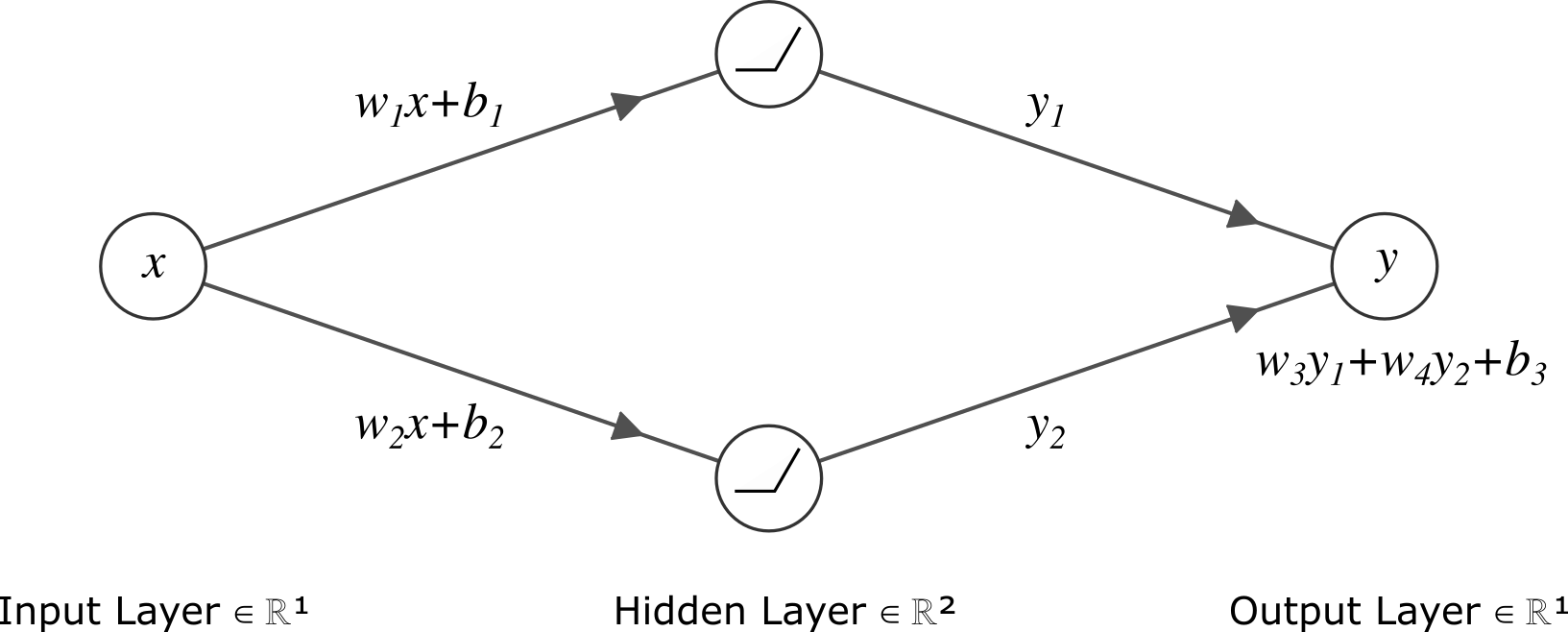
where \(y_1\) and \(y_2\) are both ReLU output:
\[
y_i = \begin{cases}
w_{i}x_{i}+b_i, & \text{ if } w_{i}x_{i}+b_i > 0\\
0, & \text{ otherwise }
\end{cases}, \text{ for } i \in \{ 1, 2 \} \tag{1}
\]
For all setup, we start training with \(w_3=w_4=b_3=0\), \(w_1=1\), and \(b_1=3\). We will have exact training setup like learning rate, optimizer, and training epoch with difference only on the initialization of \(w_2\) and \(b_2\).
We will monitor the training error and \(y_1\), \(y_2\), and \(y\) versus \(x\) values for all training epochs with \(y_1\) represented by blue-dotted line whilst \(y_2\) with green-dashed line. Two gray-vertical lines represents \(x\) where value of \(w_{i}x_{i}+b_i = 0\) for \(i\in\{1,2\}\).
Having 10,000 data points, we have our loss function \(L=\sum_{i=1}^{10,000}\frac{(y-f(x))^2}{10,000}\) with back propagation until \(w_i\) and \(b_i\) as follows:
\[\begin{align*} \frac{\partial L}{\partial w_i} = & \frac{\partial L}{\partial y_i} \frac{\partial y_i}{\partial w_i} \tag{2} \\ \frac{\partial L}{\partial b_i} = & \frac{\partial L}{\partial y_i} \frac{\partial y_i}{\partial b_i} \tag{3} \end{align*}\]
and because of Eq. (1), for \(i \in \{1, 2\}\) we have:
\[\begin{align*} \frac{\partial y_i}{\partial w_i} = & \begin{cases} w_{i}, & \text{ if } w_{i}x_{i}+b_i > 0\\ 0, & \text{ otherwise } \end{cases} \tag{4} \\ \frac{\partial y_i}{\partial b_i} = & \begin{cases} b_i, & \text{ if } w_{i}x_{i}+b_i > 0\\ 0, & \text{ otherwise } \end{cases} \tag{5} \end{align*}\]
which means that learning update for \(w_i\) and \(b_i\) only happens when \(w_{i}x_{i}+b_i > 0\) or visually when we see the training plots, these are the regions (\(R_1, R_2, R_3\)) where \(y_i\) is not flat.
3.1 Good Coverage
Here we start with \(w_2 = -1,\ b_2 = 3\), then we have our starting condition as in Fig. 3 below:
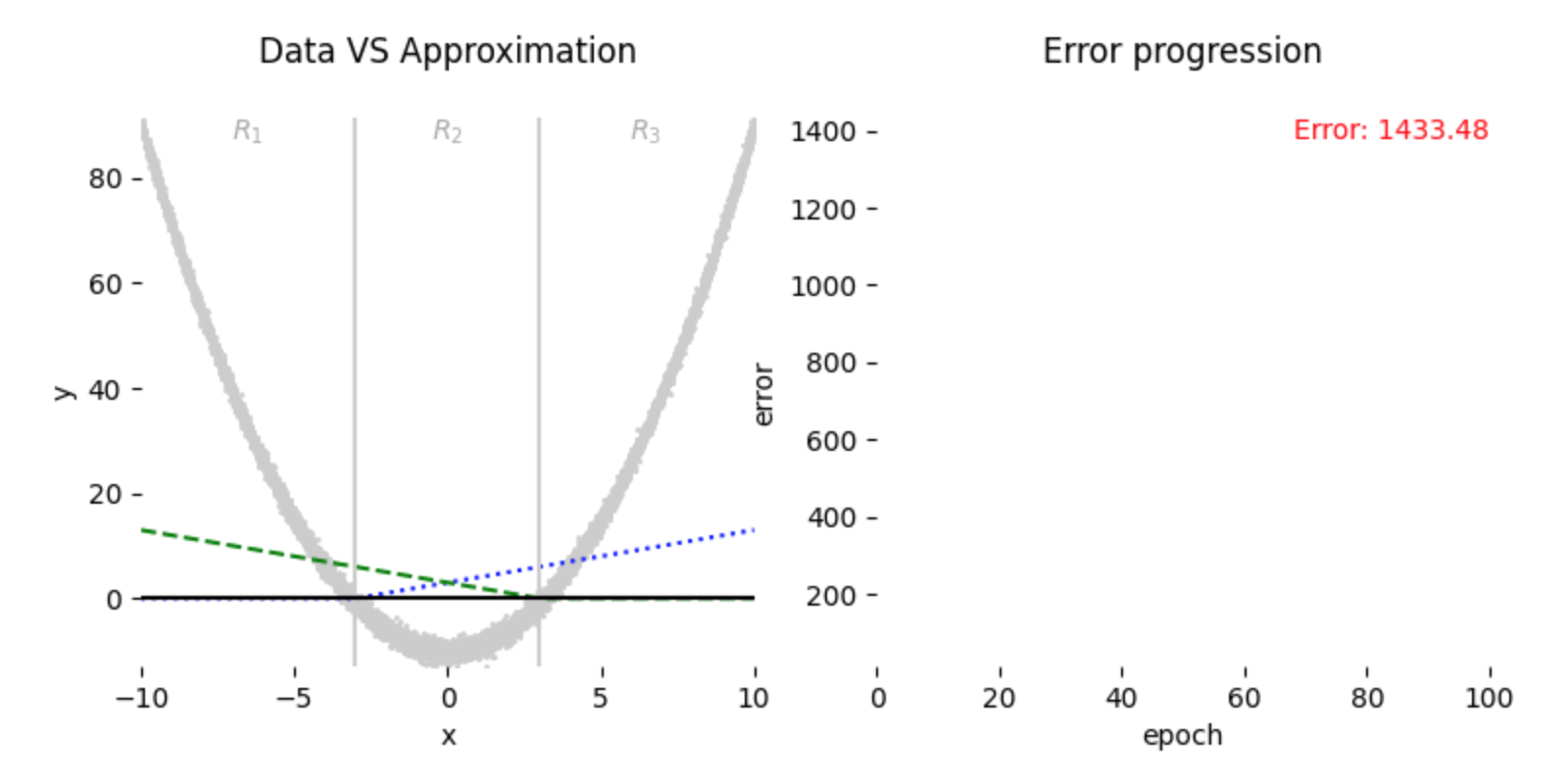
By Eq. (4) and Eq. (5), we can see that each of the region \(R_1\), \(R_2\), and \(R_3\) will contribute in updating at least one of \(w_i\) and \(b_i\) pair at initialization state which leads to decent appproximation of our data as can be seen in Fig. 4 below:
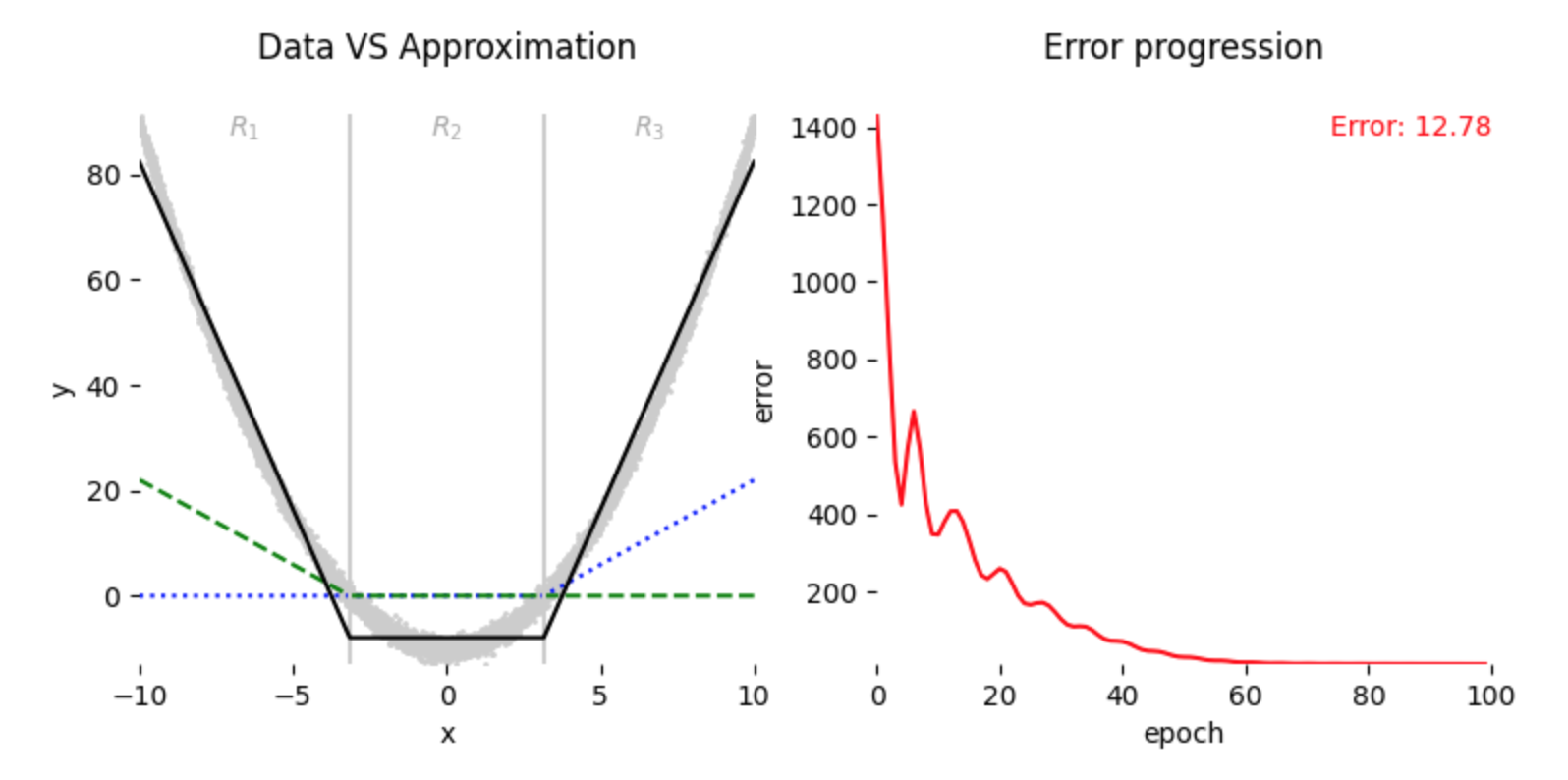
3.2 Bad Coverage
Here we start with \(w_2 = 1,\ b_2 = -3\), and here is our starting condition:
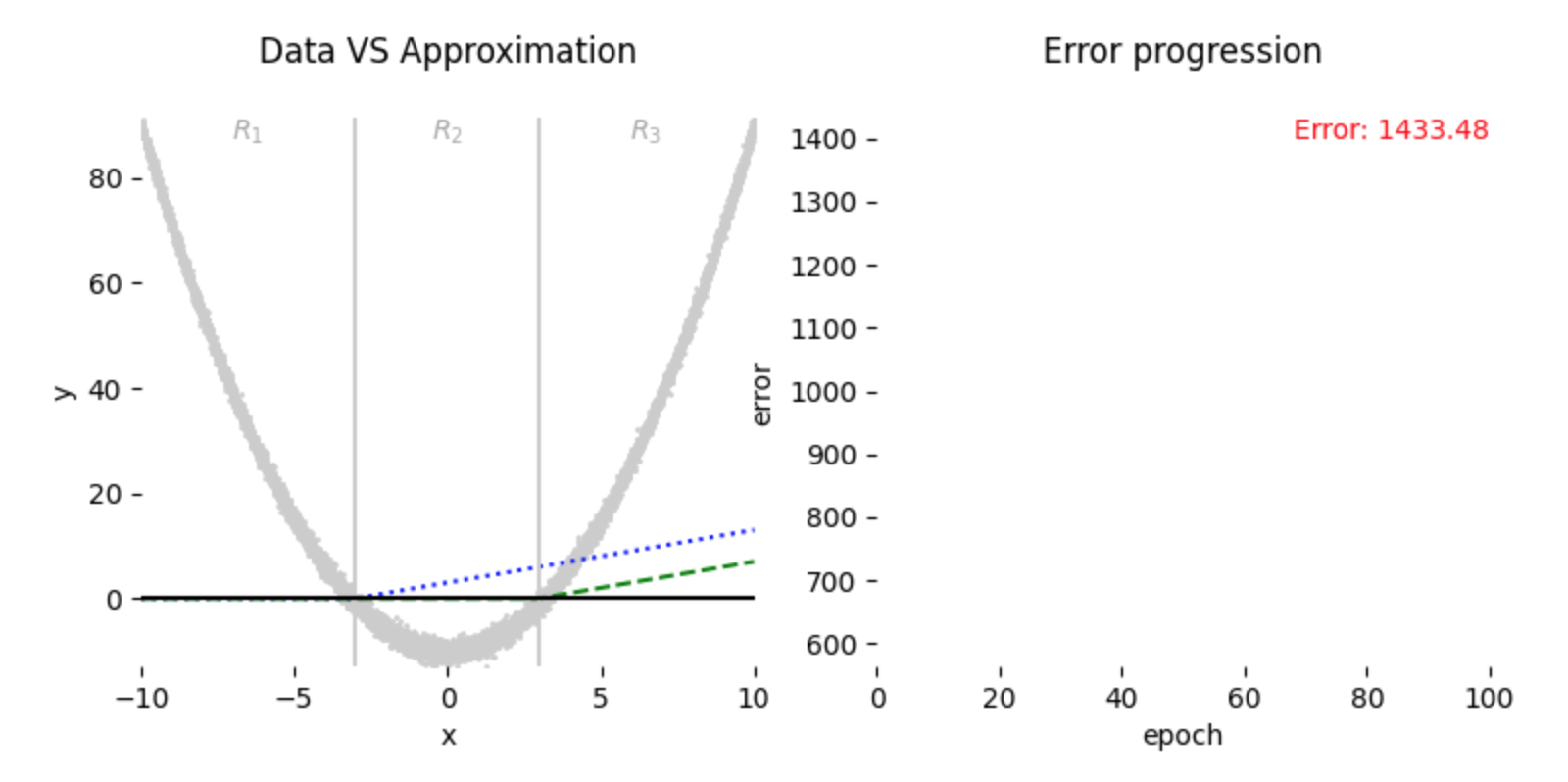
As we can see in Fig. 5 above, unlike previous setup, referring again to Eq. (4) and Eq. (5), \(R_1\) region will not contribute in updating any of \(w_i\) or \(b_i\) parameter at initialization onwards, thus ending in less optimal result:
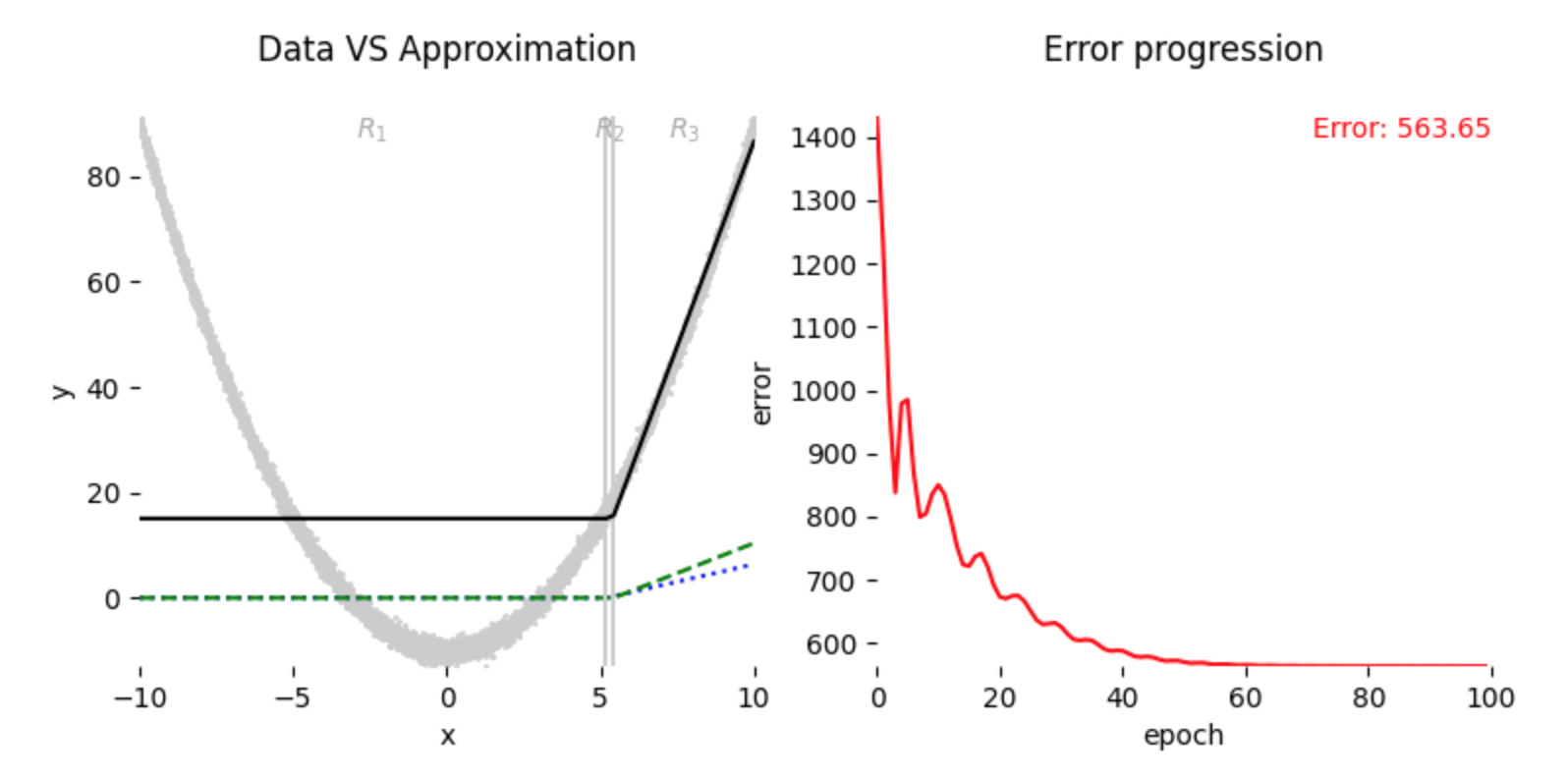
4 Conclusion
Here I’ve provided an example of Neural Network initialization gone wrong in simply what I called missing initialization coverage. Thank you for reading, got any feedback or interested in further discussion? let’s get in touch \(\rightarrow\) Email.
5 Code
All the codes can be found here \(\rightarrow\) GitHub.